Matrice de tests 2
Exemple psychométrique
La psychométrie est la science qui étudie l'ensemble des techniques de mesures pratiquées en psychologie, ainsi que les techniques de validation et d'élaboration de ces mesures. Ces techniques concernent tous les champs de la psychologie, ainsi que d'autres domaines de sciences connexes.
Moyenne par rapport à la Médiane
Il est assez difficile de décider quel agrégateur est le mieux à utiliser pour les tests, surtout en ce qui concerne la Moyenne et la Médiane.
Le mieux en matière de psychométrie est d’utiliser les deux avec un flotement de validation par les centiles.
b- Une autre pour la médiane.
c- Deux curseurs en centiles
La validation la plus fiable des tests sur le marché
Plusieurs indices et plusieurs mesures :
1- Outre les critères variable de chaque test pour chaque candidat en fonction de :
a. Déficiences de vue (lunettes/lentille) – Daltonien.
b. Défiances moteur (haut/Bas/Gauche/Droite) ou cérébrale.
c. Défiances sourd/Muet
2- La base de l’étalonnage sur l’âge du candidat :
a. < 35 ans
b. 35 – 65 ans
c. > 65 ans
Un étalonnage constant des bases de données, sur la base de toute les passation d’examen.
Une moyenne et une médiane jouent un rôle similaire dans la compréhension de la tendance centrale d'une série de chiffres.
La moyenne est traditionnellement une mesure populaire d'un point central dans un ensemble, mais elle a l'inconvénient d'être influencée par des valeurs qui sont très inférieures ou supérieures au reste des valeurs. (Données de valeurs aberrantes)
La médiane est une meilleure mesure centrale pour les cas où un petit nombre de valeurs aberrantes peut considérablement fausser la moyenne.
Pour centrer des résultats avec plus indices exemple test de coordination-bi manuelle
- Un résultat de moyenne et médiane du nombre de collisions,
- Un résultat de moyenne et médiane du temps de réalisation du test
Sur chaque test plusieurs éléments sont ainsi calculés et présenté pour une finesse de traduction.
Explication
Moyenne Médiane
Définition
Moyenne est la moyenne arithmétique d'une série de chiffres. Médiane est une valeur numérique qui sépare la moitié supérieure de
la moitié inférieure d'un ensemble.
Quand l'applique-t-on ?
La moyenne est utilisée pour des distributions normales, La médiane est généralement utilisée pour retourner la tendance
ayant un faible nombre de valeurs aberrantes. centrale des distributions asymétriques.
La médiane est généralement utilisée pour retourner la tendance
Comment calculer ?
La moyenne est calculée en additionnant toutes les valeurs et La médiane peut être calculée en répertoriant tous
en divisant la somme par le nombre total de valeurs. les numéros dans l'ordre croissant, puis le nombre dans
le centre de distribution.
Exemple: distribution Normale
2, 3, 3, 5, 8, 10, 11 2, 3, 3, 5, 8, 10, 11
(2+3+3+5+8+10+11)/7= 6
AVG = 6 MED = 5
Exemple : distribution asymétrique
2, 2, 3, 3, 5, 7, 8, 130 2, 2, 3, 3, 5, 7, 8, 130
(2+2+3+3+5+7+8+130)/8= 20 (3+5)/2=4
AVG = 20 MED = 4
Médianes en statistiques descriptives
Mode, médiane et moyenne de deux distributions différentes suivant la loi log-normale.
La médiane est principalement utilisée pour les distributions asymétriques, car elle les représente mieux que la moyenne arithmétique. Considérons l'ensemble {1, 2, 2, 2, 3, 9}. La médiane est 2, tout comme le mode, ce qui est une meilleure mesure de tendance centrale que la moyenne arithmétique égale à 3,166….
Le calcul de la médiane est couramment effectué pour représenter différentes distributions et elle est facile à comprendre, tout comme à calculer. Elle est aussi plus robuste que la moyenne en présence de valeurs extrêmes.
Propriétés théoriques optimale
La médiane est aussi la valeur centrale qui minimise la valeur moyenne des écarts absolus. Dans la série {1, 2, 2, 2, 3, 9} donnée auparavant, ce serait (1 + 0 + 0 + 0 + 1 + 7) / 6 = 1,5, plutôt que 1,944 à partir de la moyenne, qui, elle, minimise les écarts quadratiques. En théorie des probabilités, la valeur c qui minimise est la médiane de la distribution de probabilités de la variable aléatoire X.
Conclusion
Si les données étaient uniformes, nous pourrions utiliser en toute sécurité l'agrégateur Moyenne (AVG). Cependant, comme l’ensemble de chiffres contient quelques aberrants, l'utilisation de Médiane (MED) ou de filtrer les valeurs qui faussent les résultats est nécessaire.
Basé sur des données larges de population sous groupées en tranche d’âges, les données de comparaison sont alors extrêmement fiables.
Percentile des résultats encore plus précis
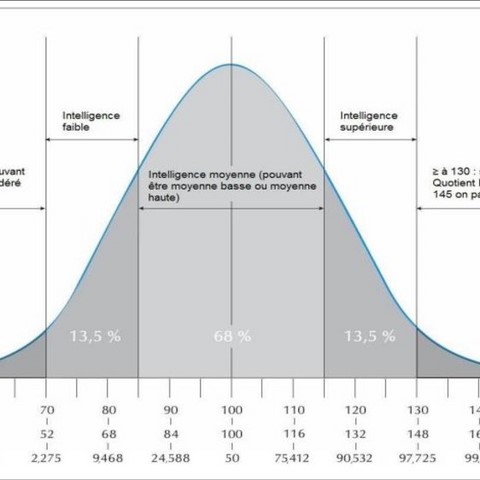
Le résultat affiché prend donc ces bases de calcules, mais qui décide si le résultat est :
- Mauvais ?
- Passable ?
- Bon ?
- Au-dessus de la moyenne ?
Sur cette matrice fine, s’ajoute des centiles (percentiles)
[Description : Multiple-choice example - ppt video online download] En statistique descriptive, un centile est chacune des 99 valeurs qui divisent les données triées en 100 parts égales, de sorte que chaque partie représente 1/100 de l'échantillon de population. Le centile fait partie des quantiles.
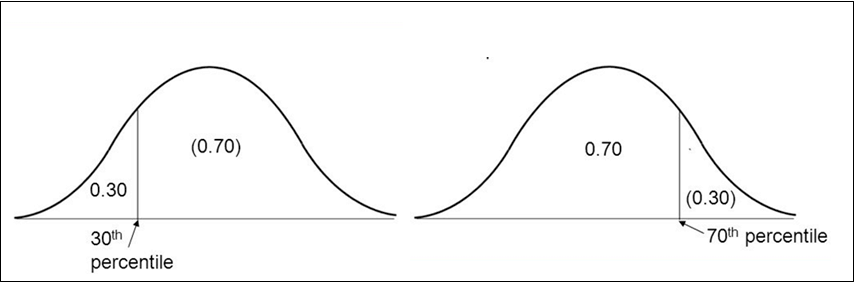
Les règles définissants les zones d’acceptabilités des résultats sont les percentiles 30 et 70, ceux-ci définissent les valeurs « entre » considérées comme résultat de : passable < bon et inférieur ou supérieur, issus de l’ensemble des passations de la tranche d’age.
L’ensemble de ces « cotes » font l’objet du de la mise à jour et étalonnage des tests, pour une fiabilité sans égal à ce jour.

